Genius Maker - School software - Maths software POLYNOMIAL EXPANSION (PASCAL'S TRIANGLE)

Polynomial Expansion Software Features:

The Polynomial Expansion is a mathematics software for finding out the expansion coefficients for each term in the expansion of (a+b)ⁿ for any user defined value of " n ". In other words, this software can be used as a tool to find out the values in any row of the Pascal's triangle.

How to start with Polynomial Expansion software ?

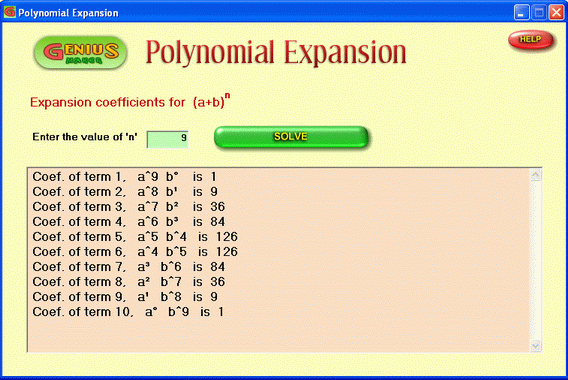
• Open Genius Maker software and click "Polynomial Expansion" button. It opens the Polynomial Expansion window as shown above.
• It asks you to enter the value for " n ". By default it shows a sample value.

EXAMPLE -1:

• Enter the value of n as " 3 ".
• Click "Solve" button.
• The result box displays the following

  Coef. of term 1, a³ b° is 1
  Coef. of term 2, a² b¹ is 3
  Coef. of term 3, a¹ b² is 3
  Coef. of term 4, a° b³ is 1 

• This implies the following Polynomial expansion.

   (a+b)³  =  a³ b°  + 3 a² b¹  +  3 a¹ b²  +  a° b³

• It also implies that the fourth row of Pascal's triangle is

      1        3        3        1

EXAMPLE -2:

• Enter the value of n as " 7 ".
• Click "Solve" button.
• The result box displays the following

  Coef. of term 1, a^7 b° is 1
  Coef. of term 2, a^6 b¹ is 7
  Coef. of term 3, a^5 b² is 21
  Coef. of term 4, a^4 b³ is 35
  Coef. of term 5, a³ b^4 is 35
  Coef. of term 6, a² b^5 is 21
  Coef. of term 7, a¹ b^6 is 7
  Coef. of term 8, a° b^7 is 1

• This implies the following Polynomial expansion.

   (a+b)⁷  =  a⁷ + 7 a⁶ b  +  21 a⁵ b²  + 35 a⁴ b³  + 35 a³ b⁴  + 21 a² b⁵  + 7 a b⁶  + b⁷

• It also implies that the eighth row of Pascal's triangle is

      1        7        21        35        35        21        7        1

EXAMPLE -3:

• QUESTION: 

What is the expansion coefficient of term  a²¹ b⁸  in the expansion of (a+b)²⁹  ? 

• SOLUTION: 

• Enter the value of n as " 29 ".

• Click "Solve" button. 
• Scroll the result box to the line where a²¹ b⁸ is displayed. It reads as 

  Coef. of term 9, a^21 b^8 is 4292145

• Hence the expansion coefficient of term  a²¹ b⁸  in the polynomial expansion of (a+b)²⁹ is 4292145

 

What is Pascal's Triangle ?

The Pascal Triangle is a triangle of numbers arranged in such a way that the rows of the triangle are the expansion coefficients of (a+b)ⁿ . 

The first row is the expansion coefficient of (a+b)ⁿ with n = 0. 

The second row is the expansion coefficient of (a+b)ⁿ with n = 1. 

The third row is the expansion coefficient of (a+b)ⁿ with n = 2. 

..... and so on.

The numbers constructed are arranged as shown below, which is Pascal's triangle.

1

1        1

1        2        1

1        3        3        1

1        4        6        4        1

1        5        10        10        5        1

1        6        15        20        15        6        1

1        7        21        35        35        21        7        1

1        8        28        56        70        56        28        8        1

1        9        36        84        126        126        84        36        9        1

1        10        45        120        210        252        210        120        45        10        1

1        11        55        165        330        462        462        330        165        55        11        1

GUJCET Gujarat  WBJEE West Bengal  Orissa JEE  SEE-UPTU Uttar Pradesh  MHT-CET Maharashtra  

CBSE Exam  Educational software  CET Engineering entrance exam  Free Science Software

© Copyright 2006-2012, Golden K star. All rights reserved.