Genius Maker - School software - Maths software COMPLEX NUMBER ALGEBRA

Features:

The Complex Number Algebra is a mathematics software, which facilitates for performing addition, subtraction, multiplication, division and square root operations on any given complex numbers. This software can produce solution to the problems, displaying the full calculations step by step. 

How to start with Complex Number Algebra software ?

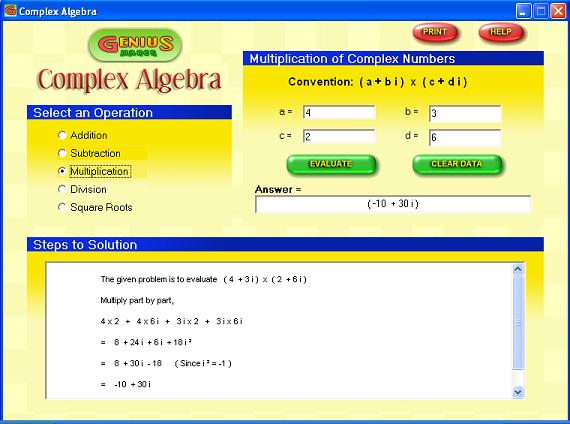
• Open Genius Maker software and click "Complex Algebra" button. It opens the Complex Algebra window.
• You may see 3 menus. One for selecting the operation, second one for entering input data as well as for display of answer and the third one for displaying the steps to solution. 
• Let us learn to use the software through examples.

Example - 1

• Find the sum of the complex numbers (4+3i) and (2+6i)

  • Click the first option "Addition" in the "Select an operation" menu.

  • The title of the top right menu should read as "Addition of Complex Numbers"
  • Click "Clear Data" button.
  • You may see the convention for entering the input data. In this case it reads as below.

  ( a + bi ) + ( c + di )

  • Hence the current problem has to be entered as a = 4, b =3, c = 2 and d= 6
  • After entering these values, click "Evaluate" button. The software displays the answer as ( 6 + 9 i )
  • The steps to solution menu shows the steps as follows.

    The given problem is to evaluate ( 4 + 3 i ) + ( 2 + 6 i )
    
    Add Real parts, 4 + 2 = 6
    
    Add Imaginary parts, 3 + 6 = 9
    
    Hence Solution is ( 6 + 9 i )

Example - 2

• Find the sum of the complex numbers ( 1 - 3i ) and ( 0 - i )

  • Click the first option "Addition" in the "Select an operation" menu.

  • The title of the top right menu should read as "Addition of Complex Numbers"
  • Click "Clear Data" button.
  • You may see the convention for entering the input data. In this case it reads as below.

  ( a + bi ) + ( c + di )

  • Hence the current problem has to be entered as a = 1, b = -3, c = 0 and d= -1
  • After entering these values, click "Evaluate" button. The software displays the answer as ( 1 - 4 i )
  • The steps to solution menu shows the steps as follows.

    The given problem is to evaluate ( 1 - 3 i ) + ( 0 - 1 i )
    
    Add Real parts, 1 + 0 = 1
    
    Add Imaginary parts, -3 + -1 = -4
    
    Hence Solution is ( 1 - 4 i )

Example - 3

• Evaluate ( 5 - 2i ) - ( 12 - 7i )

  • Click the second option "Subtraction" in the "Select an operation" menu.

  • The title of the top right menu should read as "Subtraction of Complex Numbers"
  • Click "Clear Data" button.
  • You may see the convention for entering the input data. In this case it reads as below.

  ( a + bi ) - ( c + di )

  • Hence the current problem has to be entered as a = 5, b = -2, c = 12 and d= -7
  • After entering these values, click "Evaluate" button. The software displays the answer as ( -7 + 5 i )
  • The steps to solution menu shows the steps as follows.

    The given problem is to evaluate ( 5 - 2 i ) - ( 12 - 7 i )
    
    Subtract Real parts, 5 - 12 = -7
    
    Subtract Imaginary parts, -2 - -7 = 5
    
    Hence Solution is ( -7 + 5 i )

Example - 4

• Multiply the complex numbers ( 2 - 4i ) and ( 3 + 5i )

  • Click the third option "Multiplication" in the "Select an operation" menu.

  • The title of the top right menu should read as "Multiplication of Complex Numbers"
  • Click "Clear Data" button.
  • You may see the convention for entering the input data. In this case it reads as below.

  ( a + bi ) x ( c + di )

  • Hence the current problem has to be entered as a = 2, b = -4, c = 3 and d= 5
  • After entering these values, click "Evaluate" button. The software displays the answer as ( 26 - 2 i )
  • The steps to solution menu shows the steps as follows.

    The given problem is to evaluate ( 2 - 4 i ) x ( 3 + 5 i )
    
    Multiply part by part, 
    
    2 x 3 + 2 x 5 i + -4 i x 3 + -4 i x 5 i 
    
    = 6 + 10 i - 12 i - 20 i ² 
    
    = 6 - 2 i + 20 ( Since i ² = -1 )
    
    = 26 - 2 i
    
    Hence Solution is ( 26 - 2 i )

Example - 5

• Divide the complex number ( 1 - 4i ) by ( 6 + 2i )

  • Click the fourth option "Division" in the "Select an operation" menu.

  • The title of the top right menu should read as "Division of Complex Numbers"
  • Click "Clear Data" button.
  • You may see the convention for entering the input data. In this case it reads as below.

  ( a + bi ) / ( c + di )

  • Hence the current problem has to be entered as a = 1, b = -4, c = 6 and d= 2
  • After entering these values, click "Evaluate" button. The software displays the answer as ( -0.05 - 0.65 i )
  • The steps to solution menu shows the complete step involved.

Example - 6

• Find the square root of the complex number ( 5 +12i ) 

  • Click the fifth option "Square roots" in the "Select an operation" menu.

  • The title of the top right menu should read as "Square root of a Complex Number"
  • Click "Clear Data" button.
  • You may see the convention for entering the input data. In this case it reads as below.

  Square root of ( a + bi ) 

  • Hence the current problem has to be entered as a = 5, b = 12
  • After entering these values, click "Evaluate" button. The software displays the answer as ( 3 + 2 i ) AND ( -3 - 2 i )
  • You may note that there will be 2 answers as square root for any complex number.
  • The steps to solution menu shows the complete step involved in determining the square roots.

Example - 7

• Find the square root of  " i " , where " i " is the square root of (-1)

  • Click the fifth option "Square roots" in the "Select an operation" menu.

  • The title of the top right menu should read as "Square root of a Complex Number"
  • Click "Clear Data" button.
  • You may see the convention for entering the input data. In this case it reads as below.

  Square root of ( a + bi ) 

  • The current problem is to find out the square root of (0+i)
  • Hence the current problem has to be entered as a = 0, b = 1
  • After entering these values, click "Evaluate" button. The software displays the answer as ( 0.7071068 + 0.7071068 i ) AND ( -0.7071068 - 0.7071068 i )
  • You may note that there will be 2 answers as square root for any complex number.
  • The steps to solution menu shows the complete step involved in determining the square roots.

Additional Feature:

• Print : If you want to take a printout of the soloution, it is easy. Just click the "Print" button on top. It opens the Printer dialog. Select options for printer, paper orientation and number of copies etc and then click print.

Need more Help ?

If you are not satisfied with the content of this help file and if you are in need of further help, please let us know. You may feel free to contact our support team by email.

Our email id: