Genius Maker - School software - Maths softwareFORM POLYNOMIAL EQUATIONSFROM ROOTS |  |
The Polynomial Formation is a mathematics educational software, which facilitates to find the polynomial equations from the roots. It can form polynomial equations upto fourth order. ( ie., Quartic Equations). Also this software supports for complex number roots as well as for complex numbers in the formed equations.
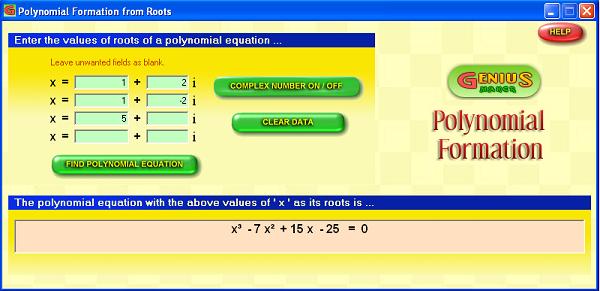
- Open Genius Maker software and click "Polynomial Formation" button. It opens the Polynomial Formation window.
- You may see 2 menus, the first one for entering the values of roots (input) and the second one displays the resulting equation (output).
Example - 1
- Find the polynomial equation, whose roots are 1, -3 and 5.
Enter the values 1, -3 and 5 in the first 3 boxes in the input field. Leave the fourth box as blank.
- Click "Find Polynomial equation" button.
- You can see the result appearing in the second menu as shown below.
x³ - 3 x² - 13 x + 15 = 0
This is the required polynomial equation with roots as 1, -3 and 5.
Example - 2
- Find the quadratic equation, whose roots are 4 and -5.
Click "Clear Data" button.
- Enter the values 4, and -5 in the first 2 boxes in the input field. Leave third and fourth box as blank.
- Click "Find Polynomial equation" button.
- You can see the result appearing in the second menu as shown below.
x² + 1 x - 20 = 0
This is the required quadratic equation with roots as 4 and -5.
Example - 3
- Find the resulting cubic equation, x (x+1) (x-7) = 0
Here the roots are x = 0, x = -1 and x = 7.
- Click "Clear Data" button.
- Enter the values 0, -1 and 7 in the first 3 boxes in the input field. Leave fourth box as blank.
- Click "Find Polynomial equation" button.
- You can see the result appearing in the second menu as shown below.
x³ - 6 x² - 7 x + 0 = 0
This is the required cubic equation which results from (x+1) (x-7) (x) = 0.
Example - 4
- Find the quartic (4th order) polynomial equation, whose roots are 2, 8, -7 and -1.
Enter the values 1, -3 and 5 in the first 3 boxes in the input field. Leave the fourth box as blank.
- Click "Find Polynomial equation" button.
- You can see the result appearing in the second menu as shown below.
x^4 - 2 x³ - 57 x² + 58 x + 112 = 0
Here X^4 means x4
This is the required quartic polynomial equation with roots as 2, 8, -7 and -1.
Example - 5
- Find the quadratic equation, whose roots are (4 + 3i) and (4 - 3i)
Click "Clear Data" button.
- Click "Complex Number ON / OFF" button. You can see the complex number fields appearing in the menu.
- Enter the value 4 in the real number field of first x value
- Enter the value 3 in the complex number field of first x value
- Enter the value 4 in the real number field of second x value
- Enter the value -3 in the complex number field of second x value
- Leave third and fourth boxes of both real and complex fields as blank.
- Click "Find Polynomial equation" button.
- You can see the result appearing in the second menu as shown below.
x² - 8 x + 25 = 0
This is the required quadratic equation with roots as (4 + 3i) and (4 - 3i).
Example - 6
- Find the cubic equation, whose roots are 3, (2 + i) and (2 - i)
Click "Clear Data" button.
- If complex number fields are not visible, click "Complex Number ON / OFF" button. You can see the complex number fields appearing in the menu.
- Enter the value 3 in the real number field of first x value
- Leave the complex number field of first x value as blank
- Enter the value 2 in the real number field of second x value
- Enter the value 1 in the complex number field of second x value
- Enter the value 2 in the real number field of third x value
- Enter the value -1 in the complex number field of third x value
- Leave fourth boxes of both real and complex fields as blank.
- Click "Find Polynomial equation" button.
- You can see the result appearing in the second menu as shown below.
x³ - 7 x² + 17 x - 15 = 0
This is the required cubic equation with roots as 3, (2 + i) and (2 - i).
Example - 7
- Find the cubic equation, whose roots are (2 + 3i), (1 + 4i) and (4 - 6i)
Click "Clear Data" button.
- If complex number fields are not visible, click "Complex Number ON / OFF" button. You can see the complex number fields appearing in the menu.
- Enter the value 2 in the real number field of first x value
- Enter the value 3 in the complex number field of first x value
- Enter the value 1 in the real number field of second x value
- Enter the value 4 in the complex number field of second x value
- Enter the value 4 in the real number field of third x value
- Enter the value -6 in the complex number field of third x value
- Leave fourth boxes of both real and complex fields as blank.
- Click "Find Polynomial equation" button.
- You can see the result appearing in the second menu as shown below.
x³ - (7+1i) x² + (44+21i) x - (26+104i) = 0
This is the required cubic equation with roots as 3, (2 + i) and (2 - i). You may note that the software is capable of producing equations, even if the resulting polynomial equation contains complex numbers.
If you are not satisfied with the content of this help file and if you are in need of further help, please let us know. You may feel free to contact our support team by email.
Our email id:
Download FREE Maths Science Educational Software - All Softwares in One pack |